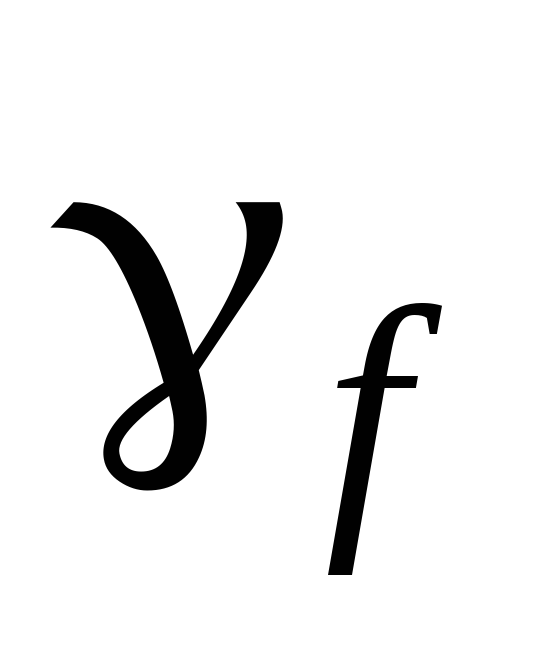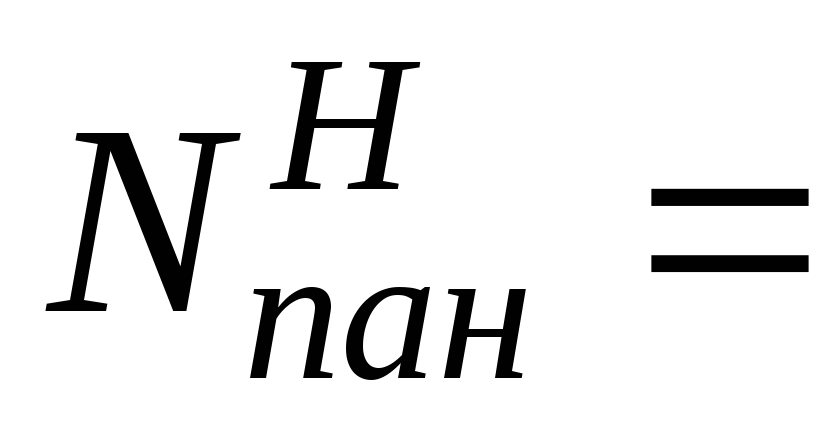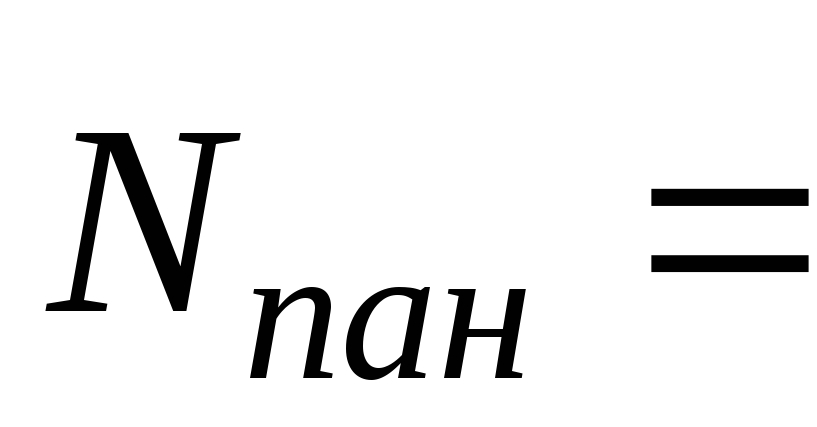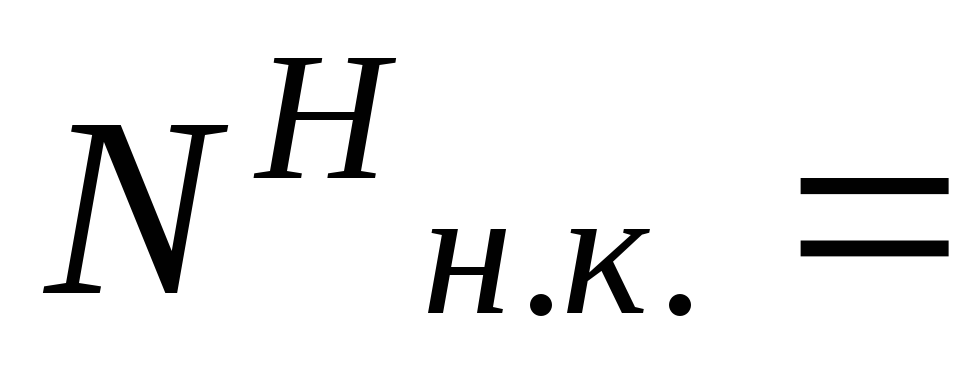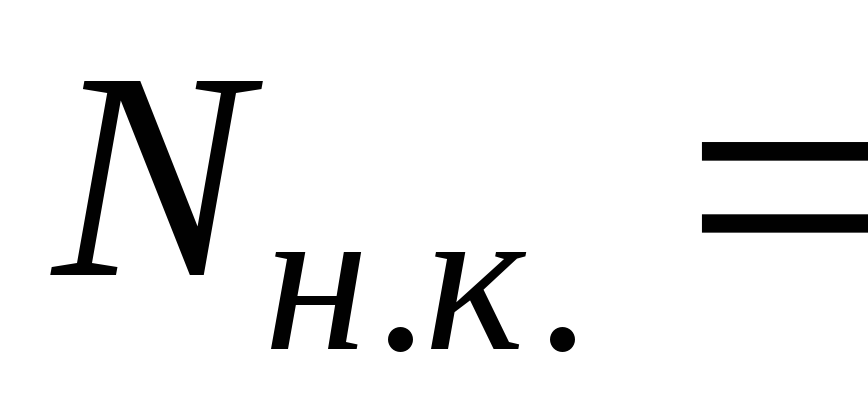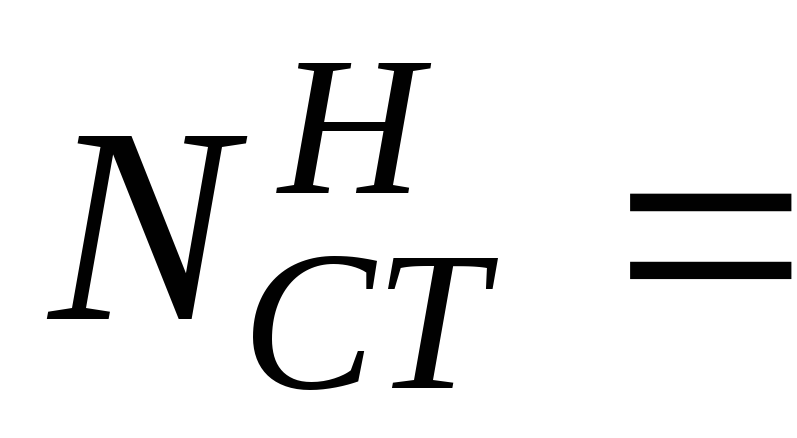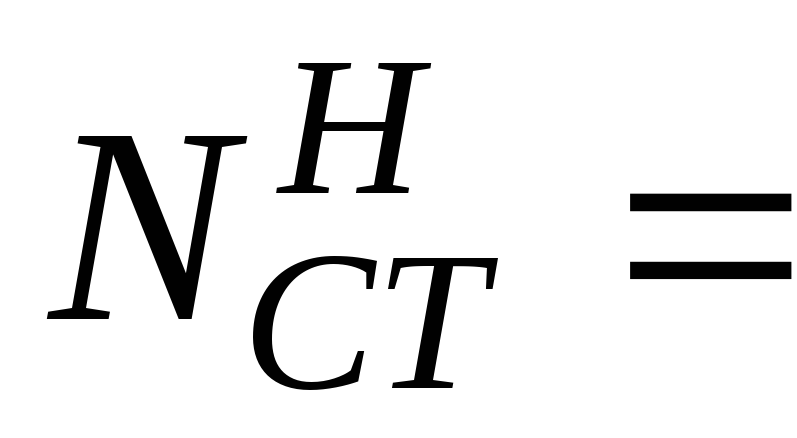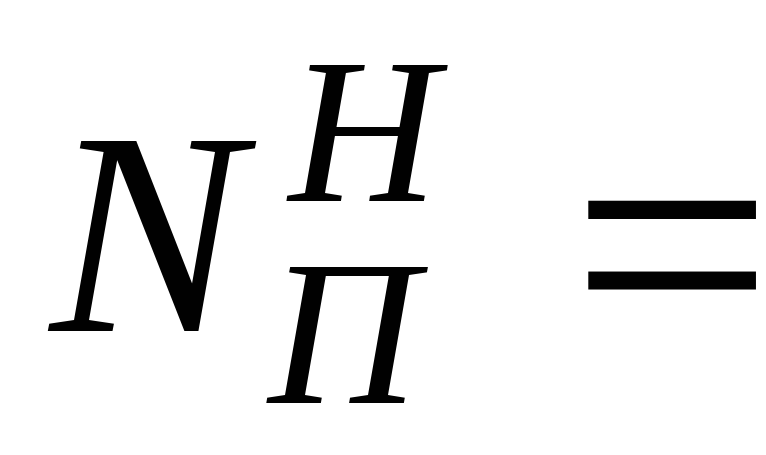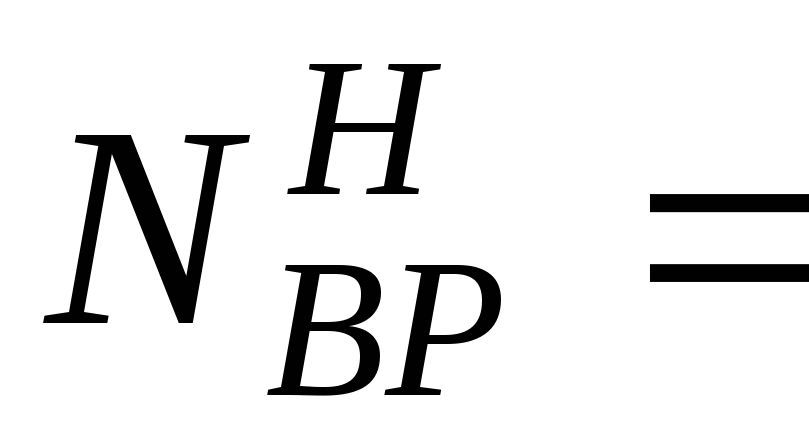Коэффициенты φ продольного изгиба центрально-сжатых стальных элементов
| Гибкость элемента | Значения φ при Ry, МПа | |||||
| 200 | 240 | 280 | 320 | 360 | 400 | |
| 10 | 0,988 | 0,987 | 0,985 | 0,984 | 0,983 | 0,982 |
| 20 | 0,967 | 0,962 | 0,959 | 0,955 | 0,952 | 0,949 |
| 30 | 0,939 | 0,931 | 0,924 | 0,917 | 0,911 | 0,905 |
| 40 | 0.906 | 0,894 | 0,883 | 0,873 | 0,863 | 0,854 |
| 50 | 0,869 | 0,852 | 0,836 | 0,822 | 0,809 | 0,796 |
| 60 | 0,827 | 0,805 | 0,785 | 0,766 | 0,749 | 0,721 |
| 70 | 0,782 | 0,754 | 0,724 | 0,687 | 0,654 | 0,623 |
| 80 | 0,734 | 0,686 | 0,641 | 0,602 | 0,566 | 0,532 |
| 90 | 0,665 | 0,612 | 0,565 | 0,522 | 0,483 | 0,447 |
| 100 | 0,599 | 0,542 | 0,493 | 0,448 | 0,408 | 0,369 |
| 110 | 0,537 | 0,478 | 0,427 | 0,381 | 0,338 | 0,306 |
| 120 | 0,479 | 0,419 | 0,366 | 0,321 | 0,287 | 0,260 |
| 130 | 0,425 | 0,364 | 0,313 | 0,276 | 0,247 | 0,223 |
| 140 | 0,376 | 0,315 | 0,272 | 0,240 | 0,215 | 0,195 |
| 150 | 0,328 | 0,276 | 0,239 | 0,211 | 0,189 | 0,171 |
| 160 | 0,290 | 0,244 | 0,212 | 0,187 | 0,167 | 0,152 |
| 170 | 0,259 | 0,218 | 0,189 | 0,167 | 0,150 | 0,136 |
| 180 | 0,233 | 0,196 | 0,170 | 0,150 | 0,135 | 0,123 |
| 190 | 0,210 | 0,177 | 0,154 | 0,136 | 0,122 | 0,111 |
| 200 | 0,191 | 0,161 | 0,140 | 0,124 | 0,111 | 0,101 |
| 210 | 0,174 | 0,147 | 0,128 | 0,113 | 0,102 | 0,093 |
| 220 | 0,160 | 0,135 | 0,118 | 0,104 | 0,094 | 0,086 |
Онлайн калькуляторы
Россия и страны СНГ
Единственный в своем роде сайт практикующего инженера, предоставляющий калькуляторы для строительного проектирования с расчетами по СП, СНиП, здесь присутствуют калькуляторы расчета железобетонных, стальных конструкций, калькуляторы расчета оснований и фундаментов.
Цель калькулона автоматизировать составление коммерческого предложения на проектные работы, по справочникам базовых цен, утверждённых правительством Москвы и России. Калькулон полезен для руководителей и сметчиков проектных организаций, он позволяет быстро определить приблизительную стоимость любых проектных работ, на которые распостраняется действие справочников базовых цен.
Интересно выполненные калькуляторы, помогут при строительстве своего каркасного дома, решат необходимость подсчета количества строительных материалов или расчета размеров той или иной детали конструкции.
Удобный бесплатный матричный онлайн калькулятор. На сайте реализованы все основные операции матричного калькулятора над матрицами, а также методы, задействующие матрицы для решения систем линейных уравнений.
Конвертируйте легко и просто!
Зарубежные
На сайте более, чем несколько сотен калькуляторов для решения сложных уравнений и формул в области электричества, механики, химии, электроники, гражданского строительства,металлургии, нефти и газа, оптики,физики, математики и др.
Вы инженер-механик, инженер-конструктор, инженер-чертежник, технический работник или студент? Нужно работать с профессиональными вычислительными системами? Но Вы не готовы или не можете платить тысячи рублей за неадекватно сложные или непонятные решения? Тогда Вам просто нужен MITCalc
Неплохие онлайн калькуляторы строительной тематики, статические расчеты балок и др.
Расчет деревянных конструкций. Эти интерактивные инструменты доступны бесплатно, чтобы помочь инженерам и архитекторам при проектировании зданий с использованием древесины в качестве материала конструкций.
Bendingmomentdiagram – это бесплатный онлайн калькулятор, который генерирует эпюры поперечных сил и изгибающих моментов для большинства простых балок. Калькулятор является полностью настраиваемым,чтобы удовлетворить большинство схем балок, что недоступно в большинстве других калькуляторов.
Прекрасно оформленный вариант калькуляторов для расчета балок из стали, древесины и опорных плит с анкерными болтами.
Быстрые решения технических задач. Выберите калькулятор ниже, чтобы начать!
Прекрасный выбор калькуляторов для расчета строительных конструкций из различных материалов.
Xcalcs — это набор инструментов для инженерных расчетов в области анализа конструкций, для непосредственного использования в веб-среде. Вы найдете его в списке под заголовком “библиотека” в оглавлении. Проверяйте почаще этот список, листы расчетов и инструменты регулярно обновляются!
Инструменты и основная информация для проектирования, инжиниринга и строительства.
Сайт практикующих инженеров содержит калькуляторы для расчета ветровых нагрузок, сейсмики, фундаментов, рам, так и отдельно, балок и колонн.
Большой выбор калькуляторов с разнообразным выбором тематики для расчета строительных конструкций, очень качественные калькуляторы сделанные практикующими инженерами.
Отличный выбор калькуляторов строительной тематики!
Здесь Вы найдете прекрасный выбор калькуляторов для расчета математики, финансов, конструкций, статистики, физики, калькуляторов преобразования единиц.
Примеры расчета стропил и обрешетки
Внимание: в текст статьи были внесены некоторые изменения с целью упрощения процедуры расчета
Дано:
Планируется такой себе двухэтажный домик 8х10 м, высота этажа 3 м (с учетом междуэтажных перекрытий). Место строительства – Московская область. Дом с пятью несущими стенами: 4 наружные и одна внутренняя, толщина наружных стен – 0.51 м, толщина внутренней стены – 0.38 м. Кровля – волнистые асбестоцементные листы. Стропильная система – двускатная кровля с опорными стойками по центральной несущей стене, шаг стропил – 1 м, обрешетка – доски необрезные толщиной 25 мм. Чердачное помещение – нежилое.
Примечание: Для большей надежности лучше сделать сплошной настил и дополнительную гидроизоляцию рубероидом перед укладкой шифера, но ограничимся расчетом бюджетного варианта.
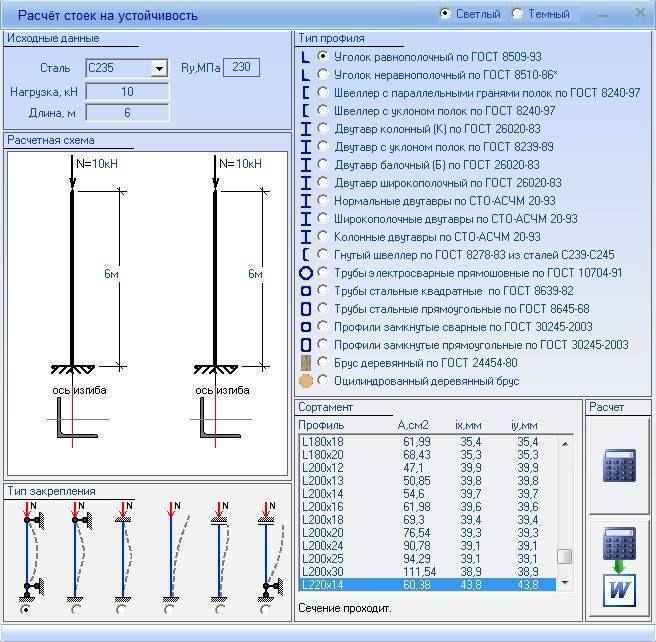
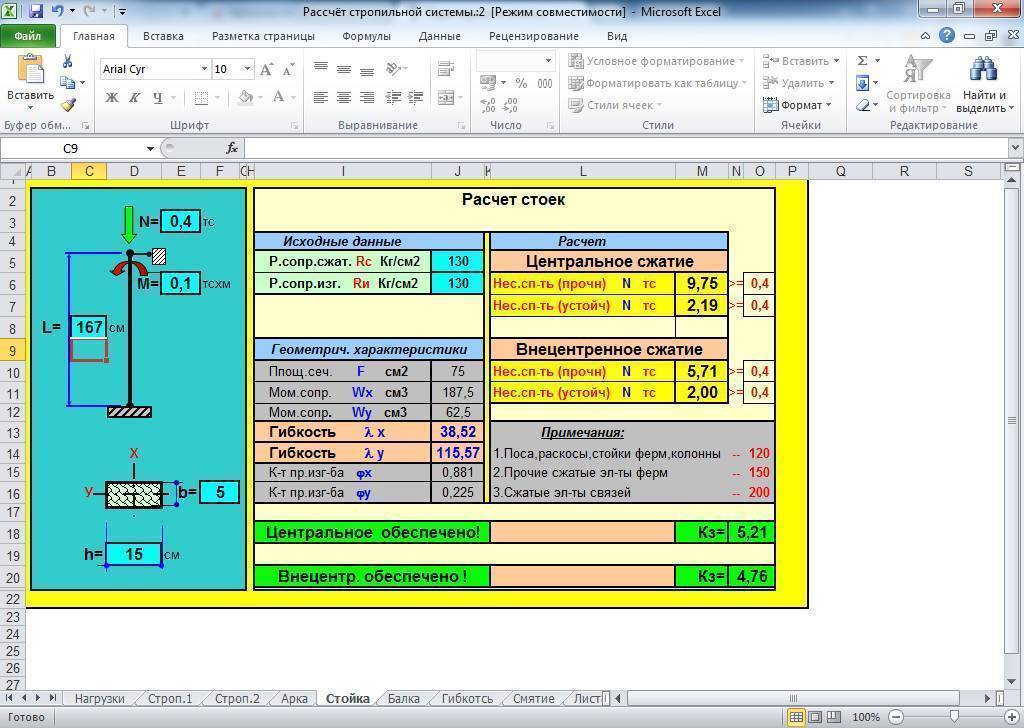
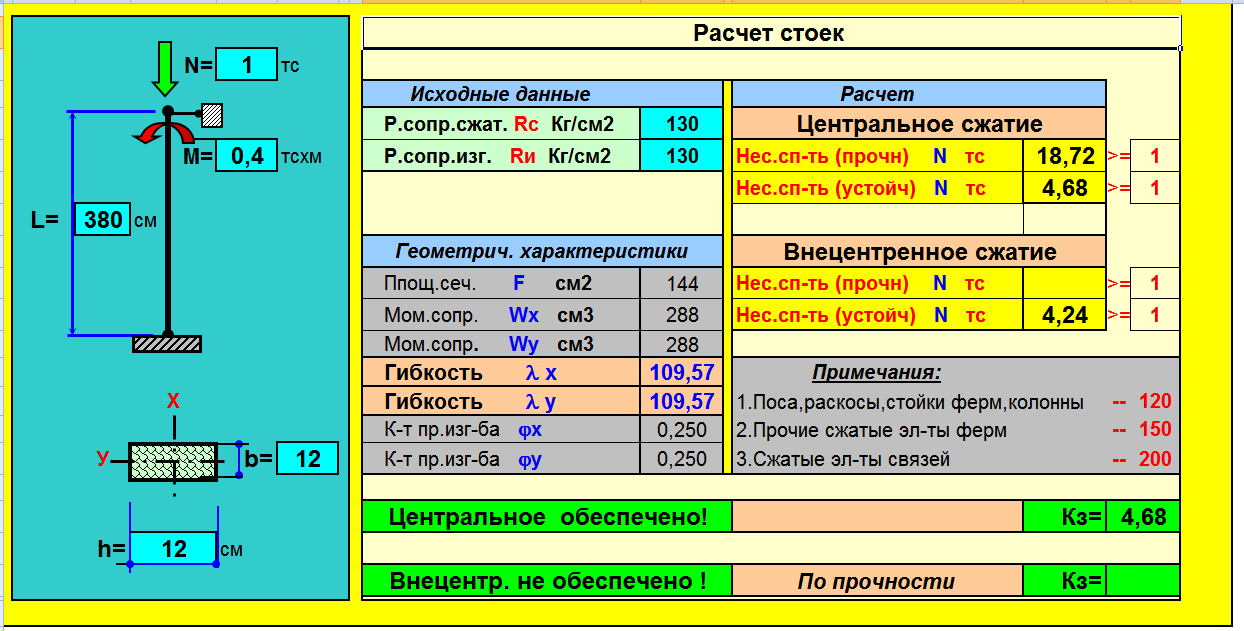
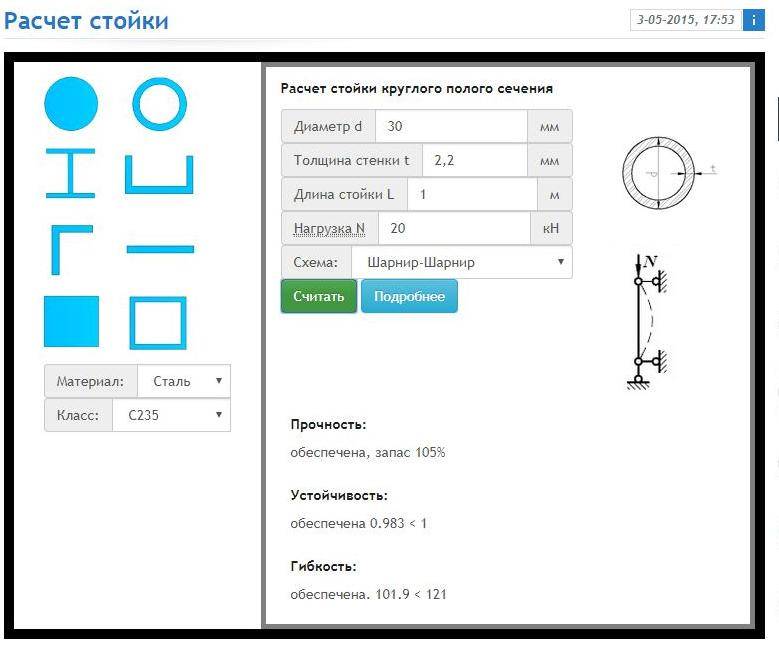
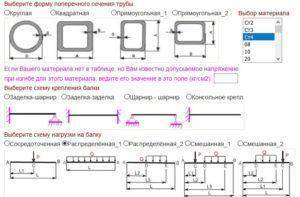
Онлайн калькулятор для расчёта стойки (колонны) из стального проката
Укажите вид проката Круг Квадрат Полоса Шестигранник Материал проката Вид и назначение стоек Если Вашего материала нет в таблице, но Вам известно расчётное сопротивление этого материала, ведите его значение в это поле (кг/см2):
Введите параметры для расчёта
| Длина стойки (колонны) L, м | Размер D или Dv, или A, мм |
| Размер B, мм | Нагрузка на стойку P, кг |
Логика онлайн расчета на прочность и устойчивость стойки из стального проката
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) рассчитывая на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P / Fp * Ry * Yc <= 1
- где P – действующая нагрузка.
- Fp – площадь поперечного сечения колонны.
- Ry – подсчетное сопротивление материала (стали колонны), выбирается по таблице В5 Приложения “В” того же СНиПа.
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi * Fp * Ry * Yc <= 1
где Fi – коэффициент продольного изгиба центрально – сжатых элементов.
Коэффициент Fi введён в качестве компенсации возможности некоторой не прямолинейности колонны, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки.
Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г., исходя из гибкости колонны и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет вычисления, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечн. сечения, в частности радиуса инерции:
Lambda = Lr / i
- здесь Lr – расчётная длина стержня,
- i – радиус инерции поперечного сечения стержня (колонны).
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где I – момент инерции, Fp – его площадь.
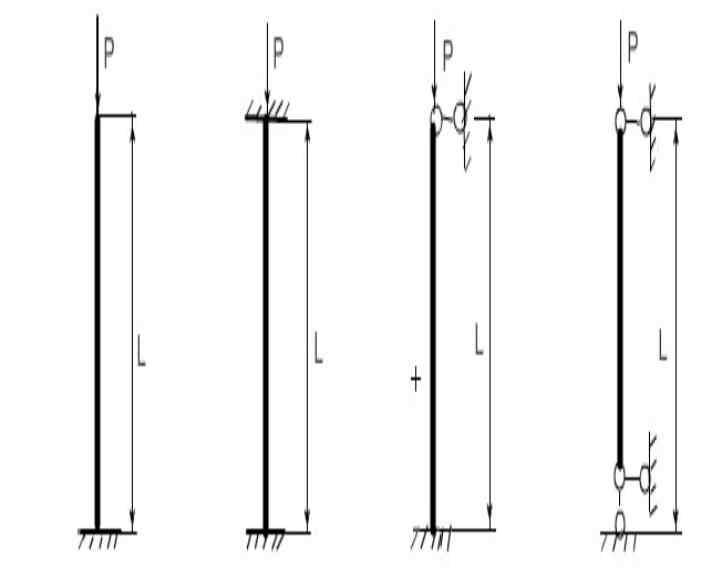
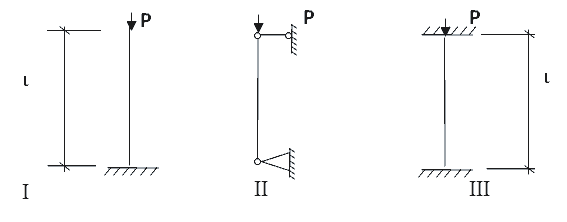
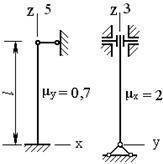
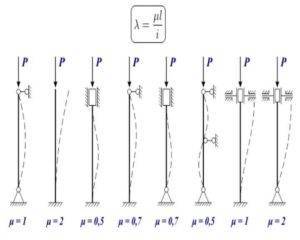
Lr (расчётная длина) определяется как Mu*L; здесь L – длина стойки, а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu=2;
- “заделка-заделка” – Mu = 0.5;
- заделка – шарнир” – Mu = 0.7;
- “шарнир – шарнир” – Mu = 1.
Следует иметь ввиду,что при наличии у формы поперечн. сечения 2-ух радиусов инерции (например, у прямоугольника), при вычислении Lambda используется меньший.
Для их использования необходимо сделать выбор в таблице онлайн калькулятора “Вид, назначение стоек”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стоики (Ry) и условий её работы (Yc).
Предельная гибкость, устойчивость и прочность стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
Приведение сосредоточенной нагрузки к эквивалентной равномерно распределенной
При расчете некоторых строительных конструкций, например, балок перекрытия, перемычек для несущих стен, стропильных ног и т.п. иногда приходится учитывать, что часть нагрузок, действующих на такие конструкции является равномерно распределенной, при этом другая часть – это условно сосредоточенные нагрузки.
Это в свою очередь означает, что расчет нужно вести по разным формулам, например, определять максимальное значение изгибающего момента отдельно для равномерно распределенной нагрузки и отдельно для сосредоточенных нагрузок. То же касается и определения максимального прогиба конструкции. Хорошо, если такая сосредоточенная нагрузка только одна, расчеты при этом не сильно усложнятся, а вот если таких сосредоточенных нагрузок несколько, да еще и приложены они на разных расстояниях друг от друга и несимметрично, то расчет становится достаточно сложным. Между тем, чем больше на строительную конструкцию действует сосредоточенных нагрузок, тем ближе суммарная эпюра моментов от этих сосредоточенных нагрузок к эпюре от равномерно распределенной нагрузки. Поэтому для упрощения расчетов конструкций постоянного по длине сечения вполне допустимо заменять сосредоточенные нагрузки на эквивалентную равномерно распределенную
Однако делать это нужно осторожно, так как варианты приложения сосредоточенных нагрузок бывают разные:
Основы сопромата
По большому счету основы теории сопротивления материалов (сопромата) даже проще, чем таблица умножения. Таблица умножения большая, ее нужно тупо заучить как “Отче наш”, а основы сопромата сводятся к нескольким основным положениям, которые достаточно легко наглядно продемонстрировать и потому их легко запомнить.
Впрочем, это мое субъективное мнение. Многие люди считают, что сопромат – это очень сложно, даже поговорка такая есть:”сдал сопромат – можно жениться”. Гуманитариям и врачам проще проштудировать перед сессией десяток увесистых томов, а людям с аналитическим складом ума проще запомнить несколько основных положений той или иной дисциплины и даже все формулы помнить не обязательно. Большинство формул можно вывести самому, пользуясь математическим аппаратом и опираясь на основные положения, во всяком случае я во время сдачи экзаменов именно так и делал.
Обстоятельства сложились так, что вступительный курс лекций по сопромату я пропустил, так как вернулся после службы на флоте в институт за 2 недели до сессии, поэтому основы сопромата пришлось постигать самому, за что самый суровый и неподкупный препод на потоке, заваливший не одну сотню студентов, поставил мне пятерку. Ну и понеслось, преподаватели, видя пятерку по сопромату, ставить меньшую отметку по своему предмету не решались и в итоге у меня получился красный диплом. Впрочем не будем отвлекаться, а вернемся к основам.
Предварительные соображения
Калькулятор предусматривает расчёт балок из некоторых видов проката на изгиб и прогиб для различных схем их крепления и нагрузки. Нагрузка балок может быть распределённой (“q” на схемах 3, 4, 5, 9, 15 и других) или сосредоточенной (“P” на схемах 1, 2, 6, 7, 8 и других.)
Крепление балок может быть:
- консольным с жесткой заделкой одного из концов (например, схемы 1, 2, 3 и другие);
- “заделка – заделка”, когда оба конца балки жестко защемлены (заделаны), схемы 6, 7, 8, 9;
- “шарнир – шарнир”, (схемы 12, 13, 14, 15 и другие), причём левый шарнир неподвижный а правый подвижный;
- “заделка – шарнир”, (схемы 9, 10, 11 др.)
Жесткая заделка балки предотвращает ее поворот и перемещение в любом направлении. Неподвижный шарнир допускает только поворот балки в месте крепления в вертикальной плоскости. Подвижный шарнир допускает поворот балки в месте крепления в вертикальной плоскости и перемещение вдоль её собственной оси. Эти перемещения весьма незначительны и являются следствием деформации балки под нагрузкой.
Основным видом этой деформации является её прогиб, величина которого наряду с приложенной к балке нагрузкой зависит также от ее длины, размеров её поперечного сечения и физических характеристик материала, в данном случае от его модуля упругости (“E”).
Из размерных характеристик поперечного сечения балки для расчёта прогиба используется момент инерции сечения (“I”); величина прогиба зависит также от положения проверяемой точки балки относительно опор. Допустимая величина прогиба балок определяется их назначением и местом в строительных конструкциях и регламентируется соответствующим СНиП; в легких случаях она не должна превышать 1/120 – 1/250 длины балки.
В связи с чем настоятельно рекомендуем проверять результаты расчета на допустимость после использования калькулятора.
С помощью нашего онлайн калькулятора вы сможете рассчитать:
- Допускаемое напряжение при изгибе (кг/см2).
- Максимальный изгибающий момент (кг/см).
- Момент сопротивления изгибу (см3).
- Осевой момент инерции поперечного сечения (см4).
- Максимальный прогиб (см).
- Расчётное напряжение при изгибе (кг/см2).
Построить дом невозможно без использования разделяющих перекрытий. Одно из них отделяет дом от наружного пространства снизу, второе – сверху. На них монтируются пол, и потолок здания, производится утепление. Горизонтальные перемычки должны выдерживать собственный вес, а также переносить нагрузки от мебели, оборудования и людей в здании.
Пример расчета треугольной фермы
При расчете промышленных ферм, перекрывающих большие пролеты и работающих под большими нагрузками, может использоваться до 10-15 видов сечений, точнее профилей с различными параметрами сечения. Это связано с тем, что напряжения в стержнях фермы разные и потому максимально точный подбор сечения при промышленных объемах производства ферм дает ощутимую экономию. В частном же строительстве при изготовлении ферм используются 1-2, максимум 3 вида сечений, не только из экономических, но и из эстетических соображений и потому достаточно рассчитать максимально нагруженные стержни и по этим показателям принимать сечение для остальных стержней фермы. В общем виде это может выглядеть примерно так:
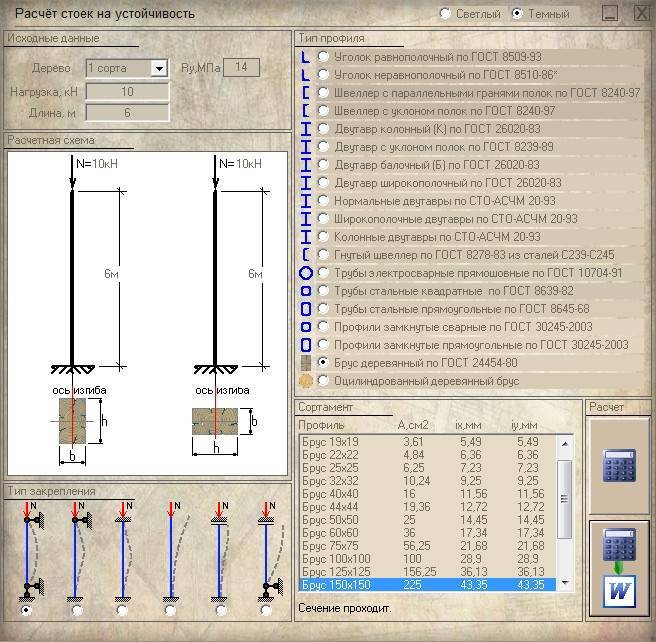
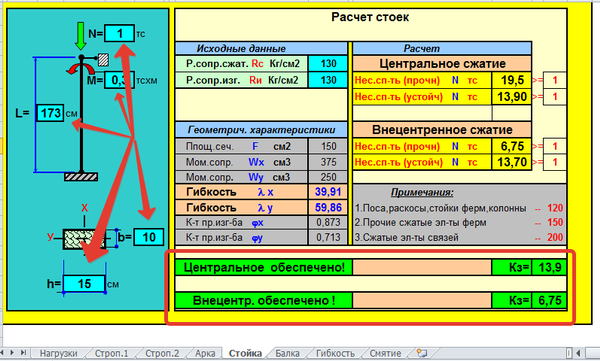
Расчет деревянной стойки на сжатие. Общие положения.
Деревянные стойки и колонны, не смотря на обилие металлопроката, железобетона и пластика, по-прежнему востребованы. Приятно иметь в саду деревянную беседку или навес во дворе. Как правило сечение элементов таких беседок или навесов подбирается из эстетических (архитектурных) соображений, но просчитать несущие элементы таких сооружений и в частности колонны или стойки на прочность не помешает, так как исторически сложившиеся архитектурные каноны приблизительно одинаковы по всей стране, а вот нагрузка на конструкции может быть ощутимо разной. Это же относится и к опорным стойкам, а также подкосам стропильных систем, да и любых других деревянных ферм.
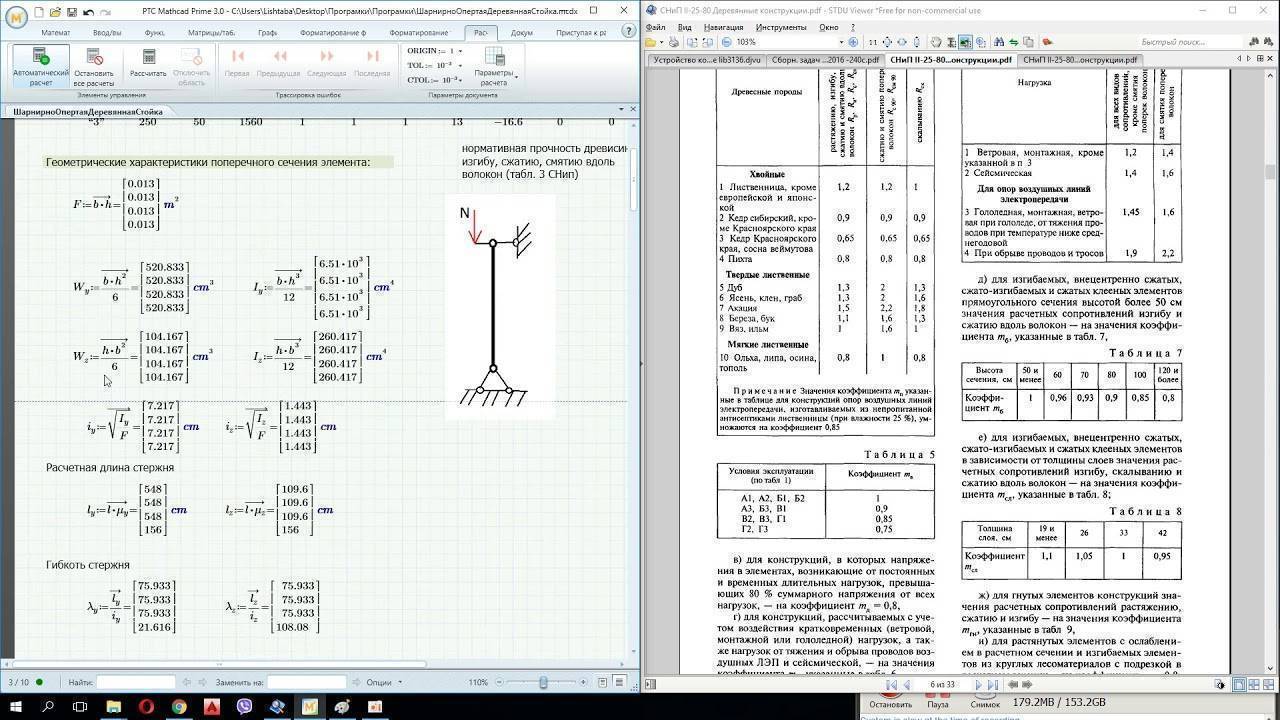
Все основные требования по расчету деревянных колонн, стоек, подкосов и любых других элементов, работающих на центральное или внецентренное сжатие, можно найти в СНиП II-25-80 (1988). А в данной статье лишь максимально упрощенно изложены основные принципы расчета сжимаемых деревянных элементов, не более того.
Момент инерции
Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.
При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба
Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:
J=b*h^3/12, где:
b – ширина сечения;
h – высота сечения балки.
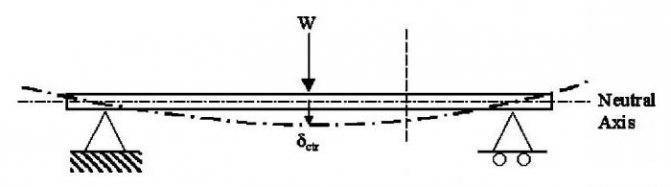
Вычисление значения максимального прогиба
Когда проводится расчет балки, формула отображает в себе все необходимые элементы. При этом стоит учитывать, что формула, используемая для расчетов, может иметь несколько иной вид, если расчет проводится для разных типов нагрузок, которые будут оказывать влияние на балку.
Сначала приведем вашему вниманию формулу, используемую для расчета максимального прогиба деревянной балки с распределенной нагрузкой.
f=-5*q*l^4/384*E*J.
Обратите внимание, что в данной формуле Е – это постоянная величина, которая получила название модуль упругости материала. Для древесины эта величина равна 100 000 кгс/ м²
Продолжив вычисления с нашими данными, использованными для примера, получим то, что для балки из древесины, сечение которой составляет 0,15х0,2 м, а длина равна 4 м, величина максимального прогиба при воздействии распределенной нагрузки равна 0,83 см.
Обращаем внимание, что когда производится расчет прогиба с учетом схемы с сосредоточенной нагрузкой, формула приобретает следующий вид:
f=-F*l^3/48*E*J, где:
F – сила давления на брус.
Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса
Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.
Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.
Пошаговая инструкция проведения расчета
1.Вводят тип проката: круглый, квадратный, в форме полосы, шестигранника и т.д.
2.Указывают разновидность схемы, по которой крепится стойка: в виде заделки консоли, в виде заделки заделки, в виде заделка шарнир, либо шарнир шарнир.
3.Выбирают материал проката, к примеру: из Стали С235 — Ст3кп2, из Стали С245 — Ст3пс5 либо Ст3сп5.
4.Устанавливают разновидность стойки, ее назначение, к примеру: стойки передающие, служащие для опоры, основные либо второстепенные.
Важно! При отсутствии типа материала в таблице, а показатель его расчетного сопротивления (кг /см 2) известен, значит, следует ввести значение в специальное поле. Чтобы произвести расчет вводят:
Чтобы произвести расчет вводят:
1.Длину стойки — L, выражают в метрах.
2.Размер D либо Dv, либо A, выражают в миллиметрах.
3.Размер B, выражают в миллиметрах.
4.Нагрузку на колонну — P, выражают в килограммах.
По последней версии СНиПа II – 23 – 81 проводя расчет прочности стальных деталей, оснащенных центральным растяжением либо сжатием посредством силы Р вычисляют при помощи следующей формулы:
P : Fp Х Ry Х Yc<=1
Расчет на устойчивость детали, имеющей сплошное сечение с центральным сжатием силой Р вычисляют согласно формуле:
P : Fi х Fp х Ry х Yс<=1
В формуле:
1.Fi – значение коэффициента, указывающий на продольный изгиб, элементов центрально – сжатого типа.
 Данный коэффициент компенсирует небольшую не прямолинейность стойки, нехватку крепежной жесткости, также неточность определения нагрузки вдоль двух осей колонны.
Данный коэффициент компенсирует небольшую не прямолинейность стойки, нехватку крепежной жесткости, также неточность определения нагрузки вдоль двух осей колонны.
Параметр Fi отличается в зависимости от марки стального материла его гибкости, как правило, значение определяют по таблице No 72 из СНиПа II-23-81 за 1990 год, зависит также от показателя сопротивления материала, сжатию при расчете, изгиба и растяжения.
Данное условие делает расчет более простым, но более грубым, потому что в СНиП указаны инженерные формулы, по которым рассчитывают Fi.
 Физическая величина – гибкость стойки, по-другому Lambda, определяющая параметры стойки, которые значение длины, поперечное сечение, в том числе значение инерционного радиуса.
Физическая величина – гибкость стойки, по-другому Lambda, определяющая параметры стойки, которые значение длины, поперечное сечение, в том числе значение инерционного радиуса.
LAMBDA = Lr : i
В формуле:
Lr – значение расчётной стержневой длины.
i – значение инерционного радиуса стержневого диаметра поперечного типа.
Данная величина, обозначаемая i вычисляется, как корень квадратный из значения I : Fp, в котором I равен моменту инерции, а Fp равно площади сечения.
Lr=Mu * L,
В формуле:
Mu – коэффициент, определяемый крепежной схемой колонны.
L – значение длины стойки.
Важно! Если у прямоугольника, имеющего два радиуса инерции сечения, вычисляют Lambda, использовать следует наименьший из них. Гибкость стойки, которую рассчитывают по вышеуказанной схеме, не может быть выше значения 220 согласно таблице No 19 по СНиПу II – 23 – 81, в нем указаны максимальные показатели предельной гибкости стоек центрально-сжатого типа
Гибкость стойки, которую рассчитывают по вышеуказанной схеме, не может быть выше значения 220 согласно таблице No 19 по СНиПу II – 23 – 81, в нем указаны максимальные показатели предельной гибкости стоек центрально-сжатого типа.
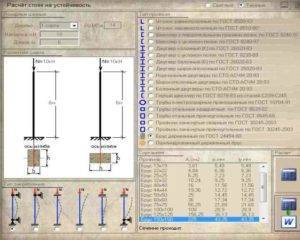
Чтобы их правильно применять, следует в калькуляторе выбрать таблицу с названием Вид и назначение стоек, далее определить подвид.
Значение предельной гибкости определяется параметрами геометрических фигур, на величину влияет изгиб продольный, нагрузка, расчетное сопротивление материала изделия, рабочие условия.
Перед тем, как начать работать в калькуляторе онлайн, следует тщательно изучить инструкцию.
Алгоритмы вычислений на онлайн калькуляторе
Изгибающий момент, который показывает калькулятор при результатах расчета балки, означает произведение силы на плечо и вычисляется по формуле:
Mmax = q × l2/8, где:
- q — нагрузка на перекрытие;
- l —длина пролета.
Момент сопротивления (требуемый) демонстрирует, насколько материал способен сопротивляться сжатию, растяжению и изгибу. В формулу вводится максимальный изгибающий момент Mmax и расчетное сопротивление древесины R. Получается Wтреб = Мmax/R, при этом R зависит от большого количества поправок, связанных с породой древесины, пропиткой и температурой, но калькулятор их не учитывает, выдавая лишь ориентировочные результаты по расчету балки.
Полезное: Рассчитываем конструкцию и пирог стен каркасного дома

Момент сопротивления балки будет разным для различных форм сечения — квадратных, круглых, прямоугольных, овальных и т. д. Прямоугольное сечение, как самое распространенное, имеет следующую формулу для определения момента сопротивления:
W = b × h2/6, в которой b и h — ширина и высота балки соответственно.
На прочность онлайн калькулятор рассчитывает, сравнивая момент сопротивления с требуемым моментом: по нормативам Wтреб ≤ W. Максимальный прогиб просчитывается по формуле:
f = (5 × q × l4 ) / (384 × E × (b × h3 / 12)), в которой нагрузка на перекрытие обозначается q, пролет — l, модуль упругости — E, высота балки h и ширина ее b.
Нагрузка на трубы круглого сечения
Применение
Круглые трубы можно встретить в любом месте. Опоры, стойки, колонны, емкости – это далеко не полный перечень использования обечаек (обечайка – металлический лист цилиндрической формы без торцов).
Кольцевой трубный профиль можно встретить при прокладке водо-, нефте-, газопроводов как в быту, так ив промышленных масштабах. Они – отличный материал для столбиков ограждений, ворот, калиток.
Благодаря наличию замкнутого контура, круглая труба обладает существенным преимуществом в сравнении со швеллерами, уголками аналогичных линейных параметров.
В результате деления первого параметра на второй, получил искомую прочность. После сравнения полученного параметра с допускаемым значением, взятого с таблицы, делают вывод о том, можно ли такую нагрузку давать на конкретный стояк, или нельзя.
Если число будет меньше допускаемого, то все хорошо. Но тут есть одно но: вычисления справедливые для растягивания, а не для сжатия.
Пользуемся калькулятором
Для варианта со сжатием круглой стойки, можно провести необходимые расчеты с использованием онлайн калькулятора.
Сначала необходимо ознакомиться с дополнительными понятиями. Сюда относят:
- Потерю общей устойчивости.
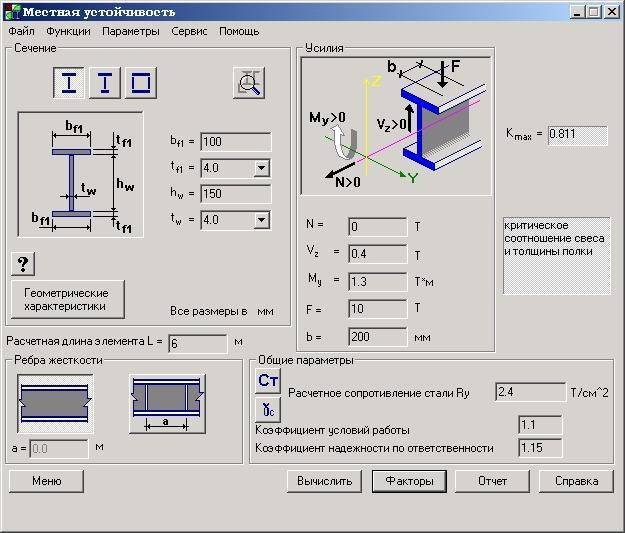
Проверка потери нужна для избегания огромных потерь иного типа. - Потерю местной устойчивости.
Речь идет о более раннем «заканчивании» жесткости стенок стояка при действии нагрузки на обечайку. Иначе говоря, труба начинает заламываться вовнутрь, а сечение круглого вида превращается в профиль неправильной криволинейной формы, что ведет к потере устойчивости.
Использование Excel
Существует специальная программа в Excel комплексной проверки расчета стояков относительно устойчивости и прочности. Основу данной программы составляют данные ГОСТа 14249 89. С ее помощью можно вычислить максимальную нагрузку на круглую трубу, а также усилия общего характера на обечайку круглого сечения.
В интернете можно часто встретить такие вопросы: «Какую нагрузку выдерживает круглая труба длиной 3, 4, 6 метров? Как это вычислить с помощью онлайн калькулятора? Можно ли это сделать самостоятельно?»
На эти и другие вопросы постараемся дать подробный ответ. Лучшим объяснением будет практический расчет величины вертикальной нагрузки на круглую трубу. Для примера, возьмем вертикальный круглый стояк диаметром 57 мм длиной 3 метра (чаще всего используется для обустройства навесов, гаражей, иных сооружений) и вычислим, какую нагрузку труба сможет выдержать.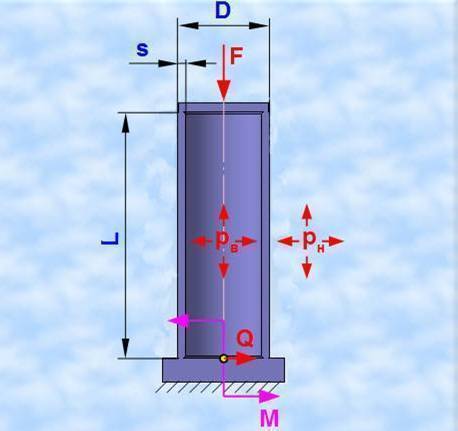
Какие данные нужны
Алгоритм работы с программой состоит в следующем:
- Сначала нужно открыть ГОСТ 14249 89, из которого необходимо выписать первых 5 исходных значений. Для быстрого отыскания параметров воспользоваться примечаниями к каждой ячейке.
- Заполнить ячейки D8, D9, D10, вписывая в них линейные параметры стояков.
- В ячейки от D11 до D15 внести возможные нагрузки.
Важно! Если на обечайку будет действовать внутреннее избыточное давление, то значение наружного давления равняется нулю. Аналогично: при воздействии на стояк внешнего избыточного давления, параметр внутреннего давления также будет равным нулю
Важно! Помните, что примечания к каждой ячейке в столбце «Значение» содержат в себе ссылку номеров нужной формулы, необходимой таблицы или чертежа из ГОСТа 14249 89
Что получилось в результате
Нужно не только уметь пользоваться программой, но также уметь объяснить полученные результаты.
Необходимо сопоставить отношение действующей нагрузки к допускаемой: при получении числа, большего за единицу, труба – перегруженная. В противном случае – заданный вес стояк выдержит, при условии, что расчет нагрузки на трубу круглого сечения проведен правильно.
Важно! Пользователь должен увидеть значение суммарного влияния всех действующих сил и давлений
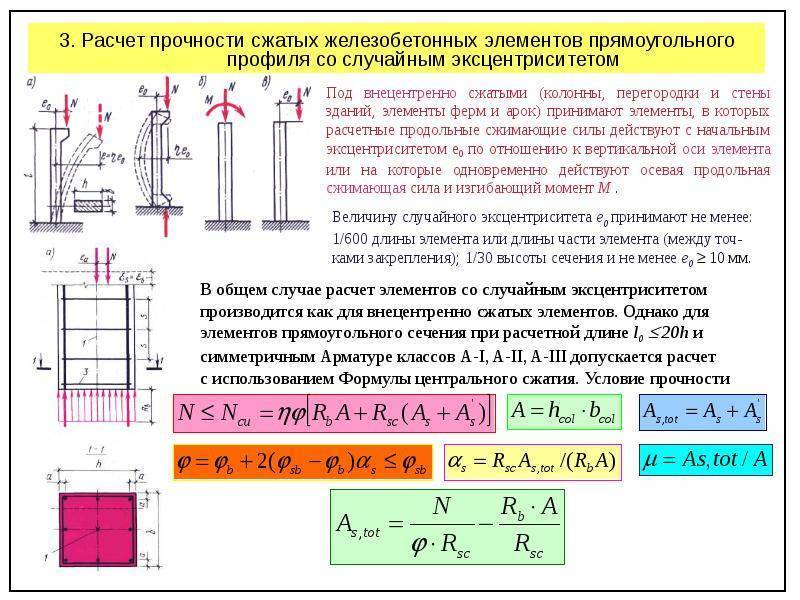
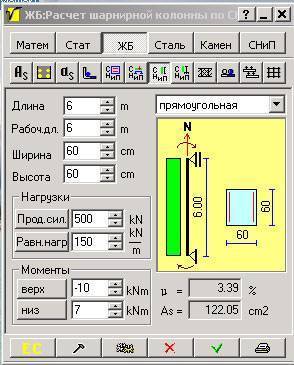
Расчет железобетонной колонны
В частном строительстве железобетонные колонны делаются не так уж и часто, а если и делаются, то как правило это центрально загруженные колонны достаточно большого сечения и относительно малой длины, да и арматуру на колонны жалеть не принято, а потому делаются такие колонны без особенного расчета и прочности им обычно хватает.
Между тем иметь хотя бы общее представление о принципах расчета железобетонных колонн не помешает, а если колонны будут внецентренно нагруженными, то без расчета уже не обойтись. Расчет следует производить согласно требований СНиП 2.03.01-84 или СП 52-101-2003. Приводимые ниже примеры расчета не более, чем примеры.
Предназначение калькулятора для определения изгиба
Для создания каркасов различных строений самое большое распространение получила древесина. Из нее, как из пластилина, можно сотворить конструкцию любой сложности. Однако далеко не последнее место занимает и такой конструкционный материал как различные металлические профили.
Их выгодно отличает такое свойство как пластичность, долговечность и прочность. Не последнее место среди таких материалов занимают профильные и круглые трубы. Попытайтесь представить себе навес для автомобиля из профильной трубы с покрытием из поликарбоната и такое же строение из уголка.
Похоже, двух мнений быть не может. А любая балка из трубы в конструкции должна быть просчитана. Это необходимо по двум причинам:
- Получить объект с достаточным запасом прочности под воздействием собственного веса, а также ветровых и снеговых нагрузок.
- Подобрать минимально допустимый для строения профиль с целью минимизировать расходы на материалы.
Для достижения этой цели необходимо воспользоваться нашим онлайн калькулятором и рассчитать балку из трубы на изгиб. Это в случае, если деталь закреплена с одной стороны (консольная). Если же закреплены оба конца, понадобится рассчитать трубу на прогиб.
При этом необходимо учитывать следующие обстоятельства:
- Размеры и сечение: (профильная или круглая). Для профильной прямоугольной трубы расчет производится с учетом направления воздействия. При расчете балок из квадратной трубы этот фактор одинаков для любого направления воздействия.
- Прочностные характеристики материала с учетом толщины стенок и марки материала. Это особенно актуально при использовании балок из круглой трубы, расчет которой в значительной степени зависит от указанных характеристик ввиду многообразия применяемых материалов.
Общие сведения
Колонны подвергаются проверке на:
1.уровень прочности.
2.на уровень устойчивости.
3.на уровень гибкости, которая может быть допустима.
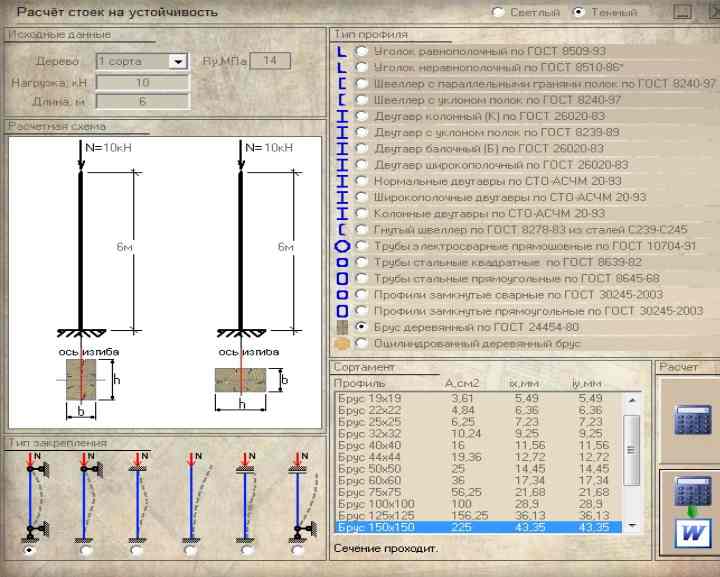
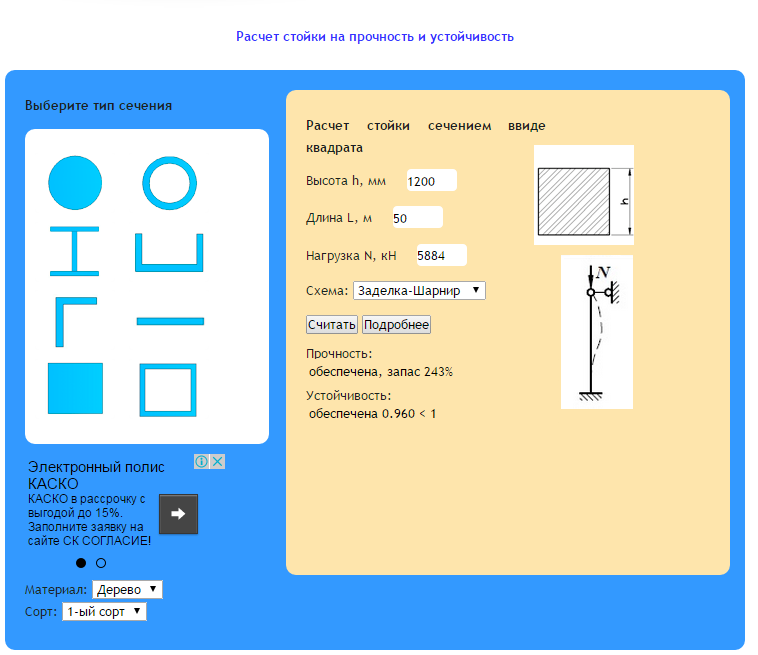
Для проведения расчетов свойств стойки можно воспользоваться онлайн – калькулятором.
Программа рассчитана на вычисление стоек, выполненных из трех материалов:
1.из дерева трех сортов.
2.из стали десяти классов.
3.из бетона девяти классов.
Программа различает такие виды сечения, как:
1.труба,
2.круг.
3.двутавр.
4.швеллер.
5.уголка.
6.сечение в виде квадрата.
7.сечение в виде прямоугольника.
8.труба с квадратным профилем.
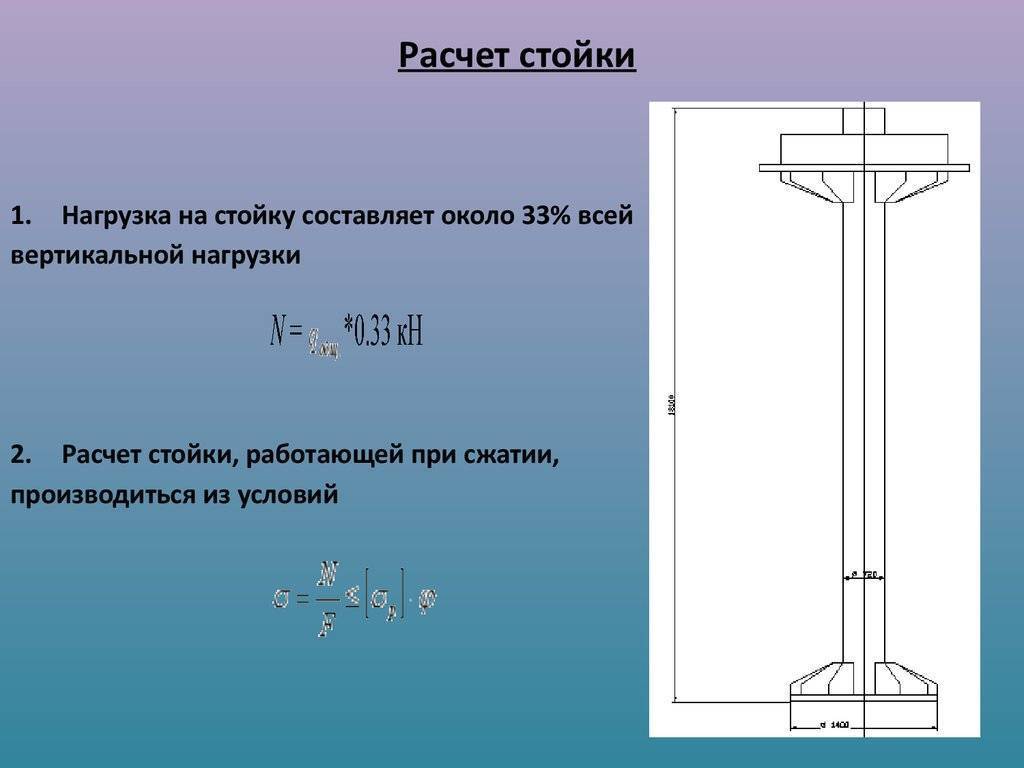
Чтобы рассчитать стойку, необходимо ввести в специальные поля размеры диаметров фигур по их геометрии, они показаны на рисунке, также нужно знать значение длины изделия, показатель расчетной крепежной схемы, задают нагрузочный параметр для колонны.
После того, как пустые поля заполнены, нажимают «считать», программой выводится на экран показатели на прочностные свойства колонны и ее устойчивость. Если надо получить расширенную информацию, нажимают «подробнее», тогда на экране появляются значения площади внутри стойки, показатель расчетного сопротивления материла, значение напряжения, значение инерционного радиуса по Х-У оси, значение гибкости по оси, показатель расчетного значения длины изделия, параметры изгибов продольного типа.
Расчет максимального прогиба для балки с двумя опорами
В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
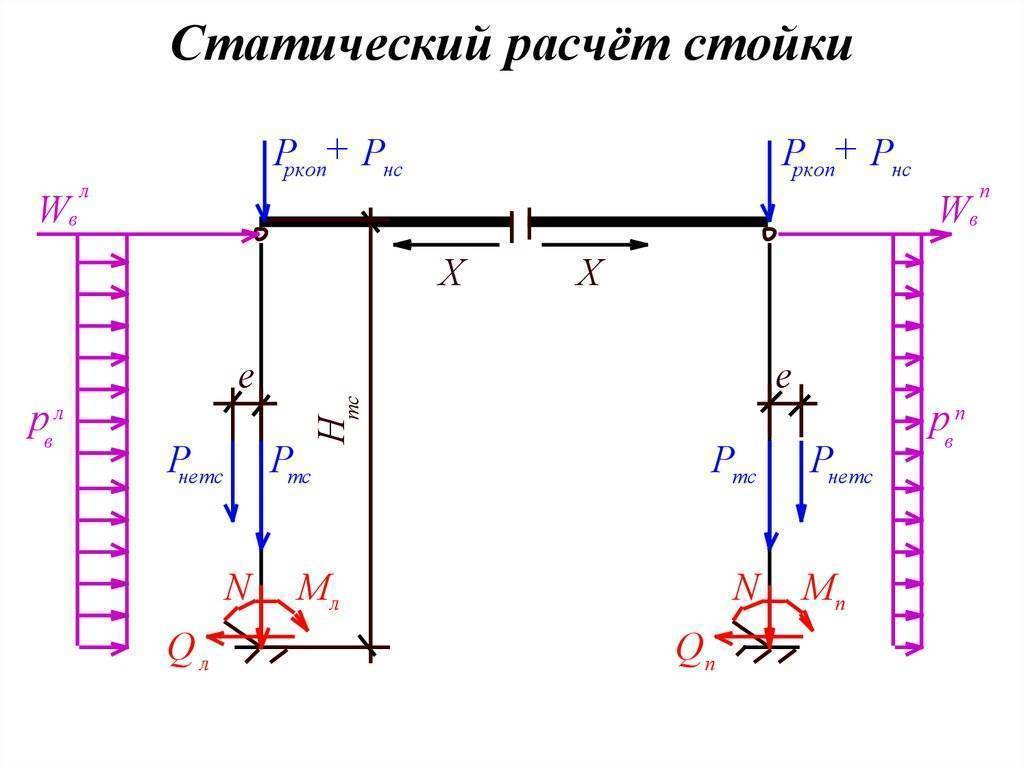
5.2. Сбор нагрузки
а)
горизонтальные нагрузки
Погонные
ветровые нагрузки
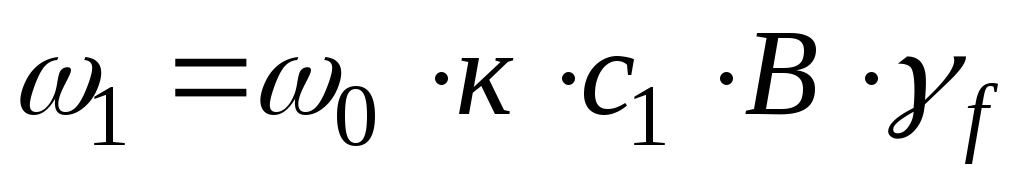 ,
,
(Н/м)
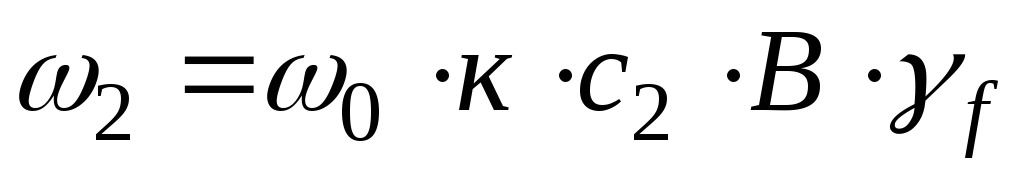 ,
,
где  – коэффициент, учитывающий значение
– коэффициент, учитывающий значение
ветрового давления по высоте (приложение
табл. 8);
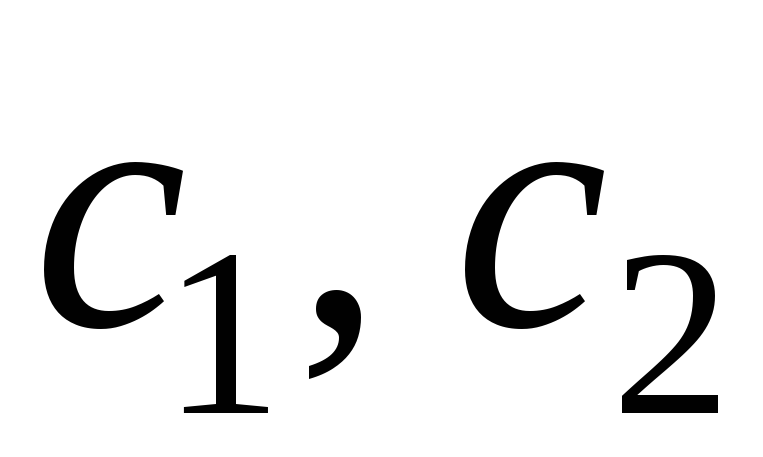 – аэродинамические
– аэродинамические
коэффициенты (при
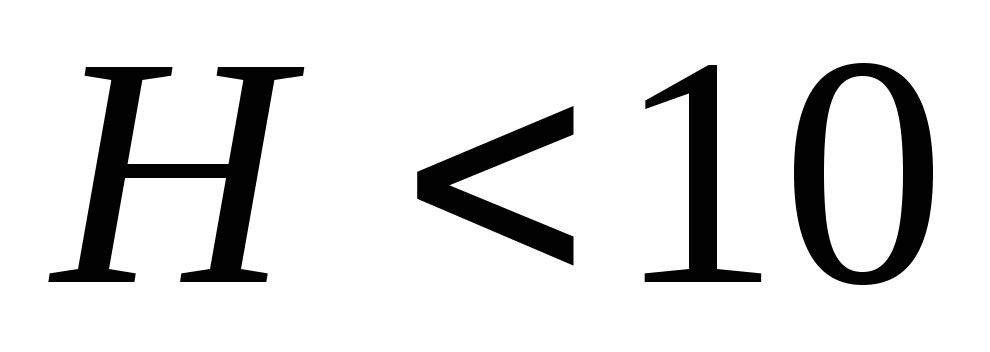 м принять
м принять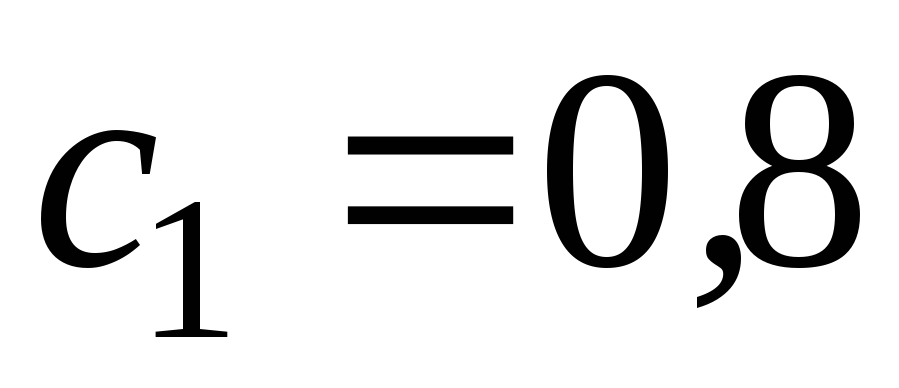 ;
;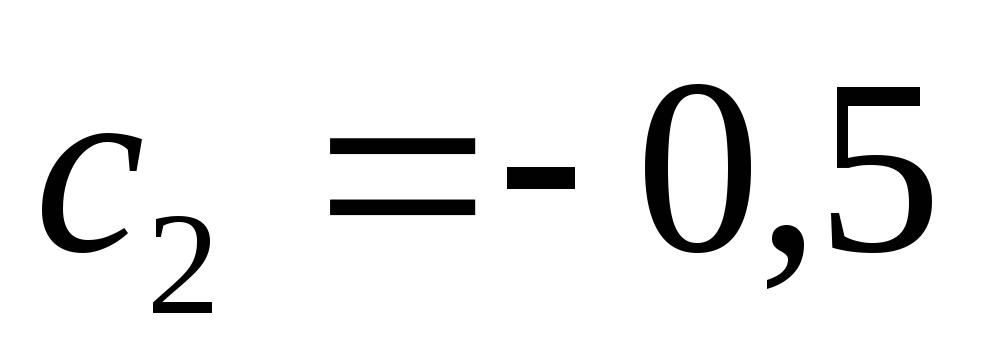 );
);
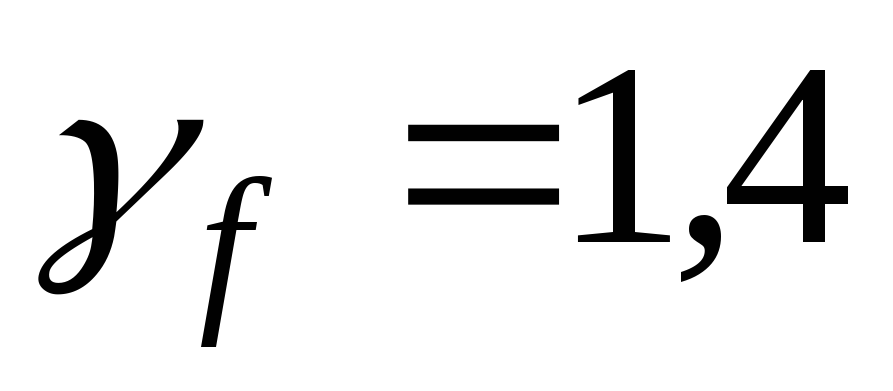 – коэффициент
– коэффициент
надежности по нагрузке;
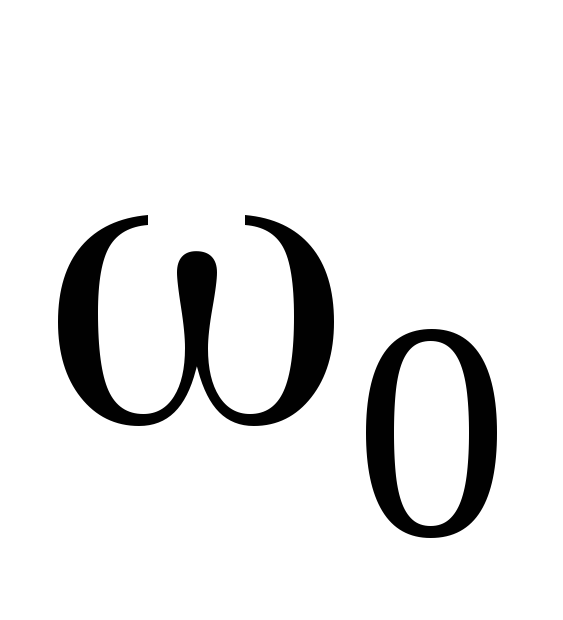 – нормативное
– нормативное
значение ветрового давления (по заданию).
Сосредоточенные
силы от ветровой нагрузки на уровне
верха стойки:
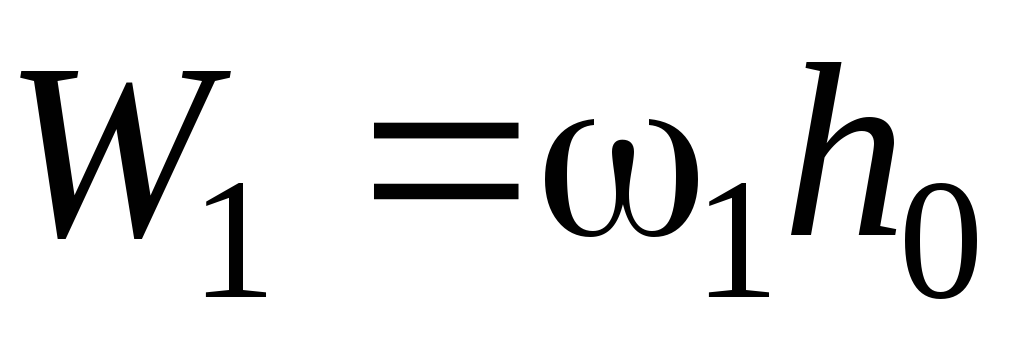 ,
,
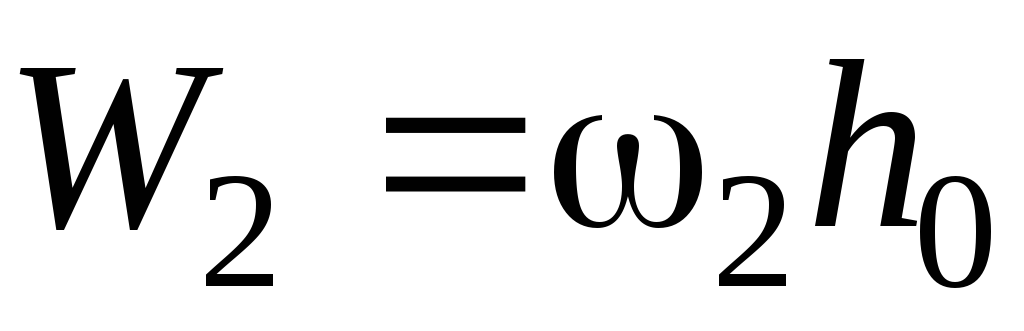 ,
,
где 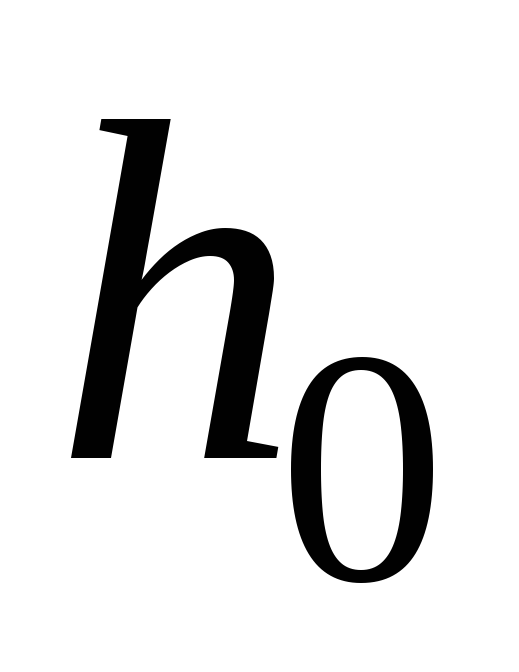 – опорная часть фермы.
– опорная часть фермы.
б) вертикальные
нагрузки
Нагрузки
соберем в табличной форме.
Таблица 5
Сбор
нагрузки на стойку, Н
Наименование |
|
|
|
Постоянная | |||
1. |
|
| |
2. |
|
| |
3. |
|
| |
Всего: |
|
| |
Временная | |||
4. Снеговая |
|
| |
|
|
Примечание:
1. Нагрузка от
панели покрытия определяется по таблице
1
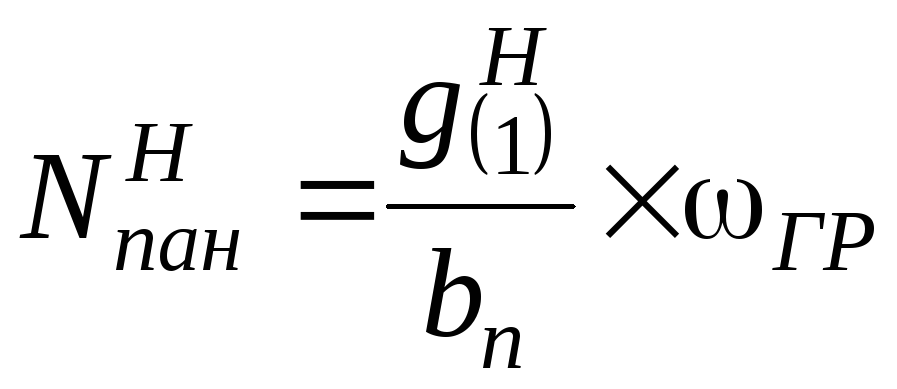 ,
,
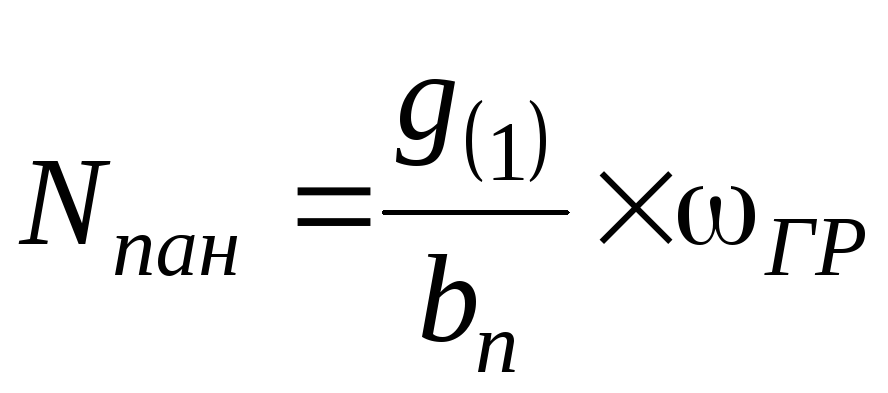 .
.
2. Нагрузки от балки
определяется
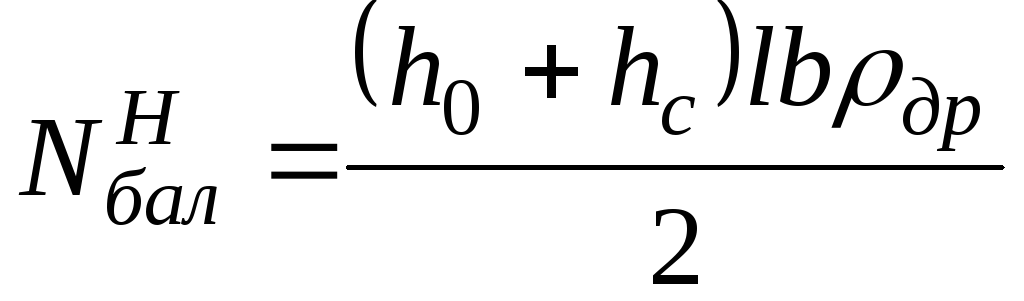
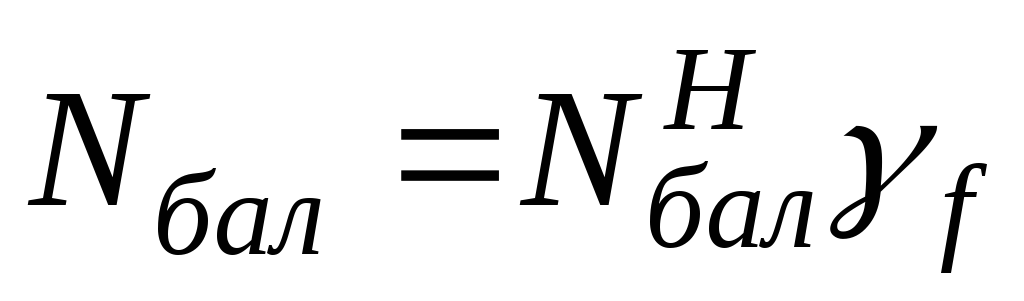 .
.
3. Собственный вес
арки
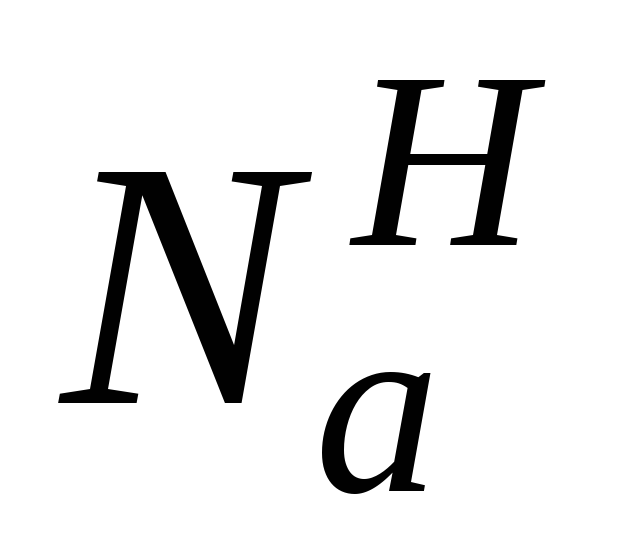 определяется:
определяется:
Верхний пояс
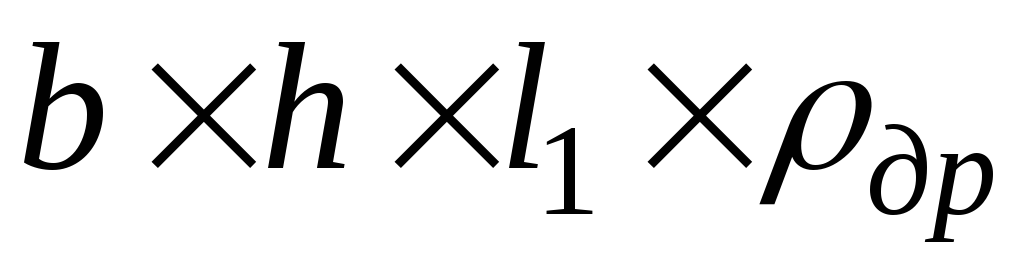 ;
;
Нижний пояс
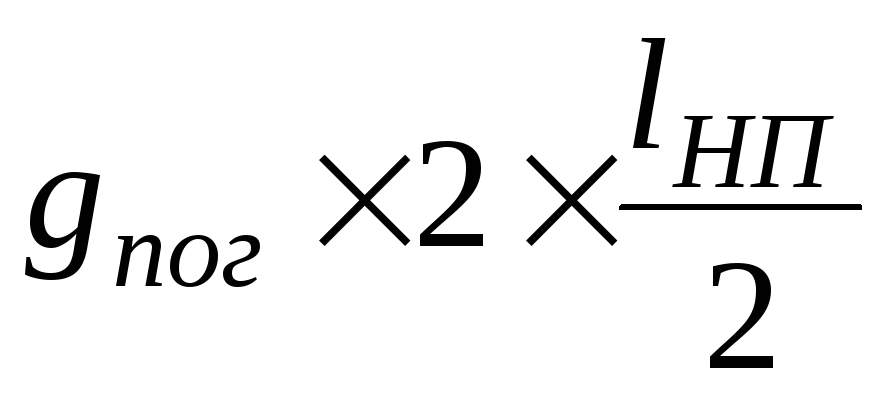 ;
;
Стойки.
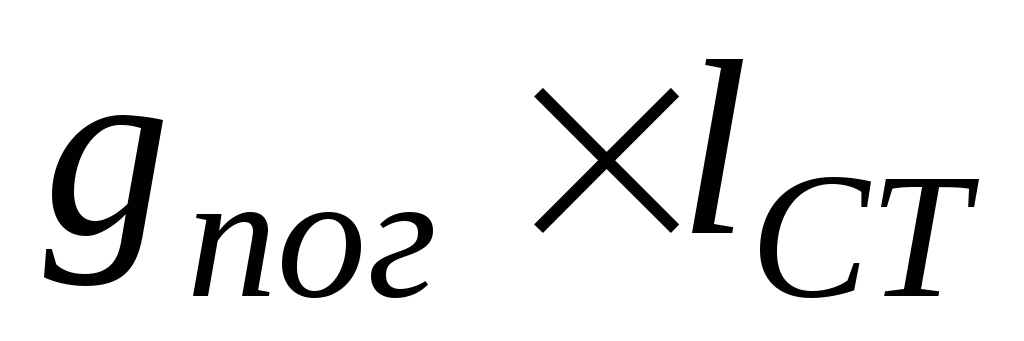
Для получения
расчетной нагрузки элементы арки
умножаются на
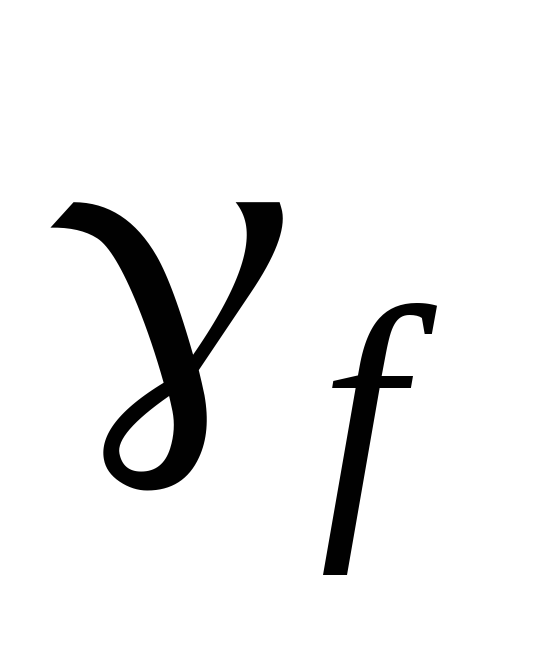 ,
,
соответствующие металлу или дереву.
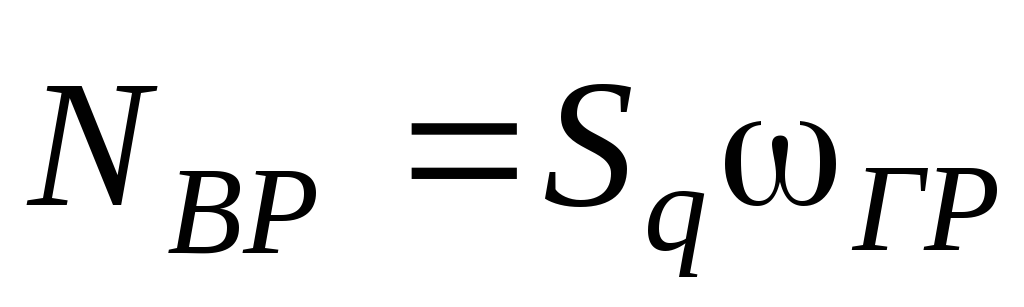 ,
,
 ,
,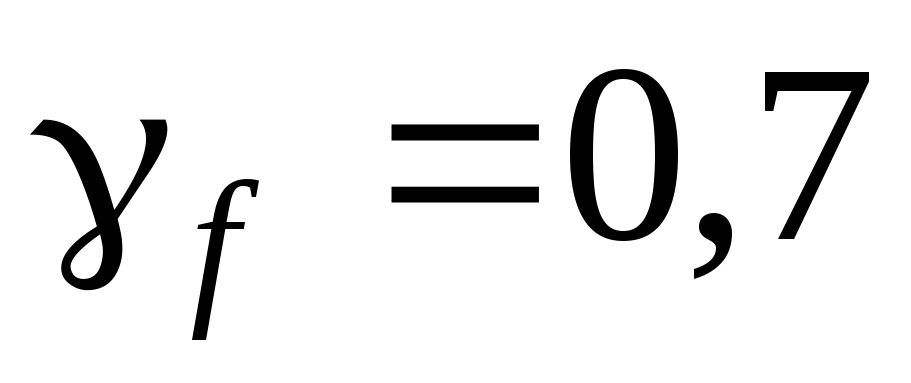 .
.
Неизвестная
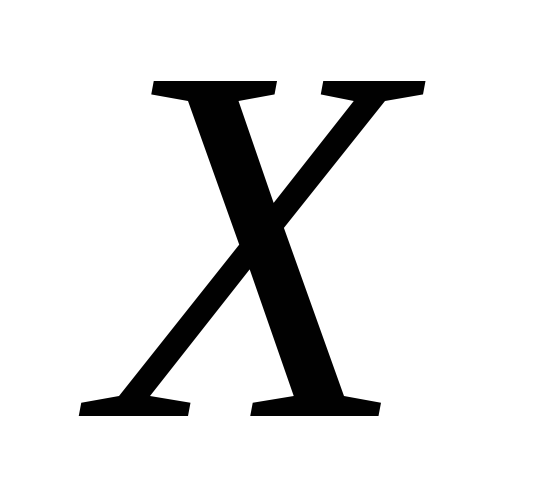 :
: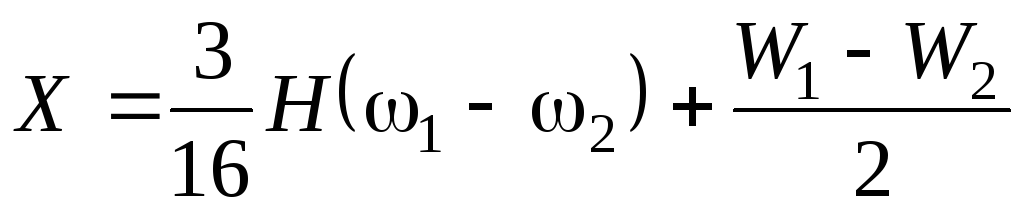 .
.
Изгибающий момент
в основании стойки
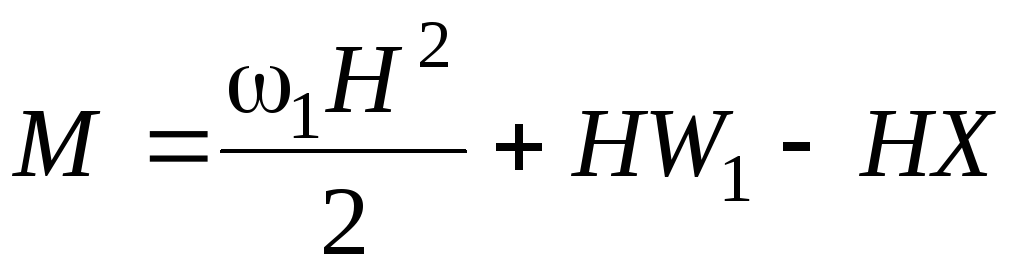 .
.
Поперечная сила
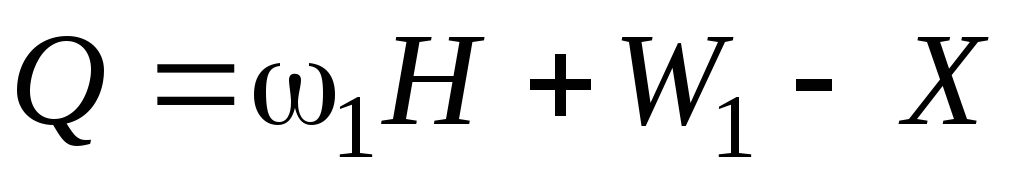 .
.